3-way PCA
Author: Chiara Magliaro (chiara.magliaro at googlemail.com);
History: 24/04/2012: First version;
Source: Download Plugin_PCA.jar, change its name to Plugin_PCA.zip and uncompress to retrieve the source code.;
Installation: copy Plugin_PCA.jar in Imagej’s “plugins” folder, then run Imagej;
Description: The 3-way PCA is a generalization of PCA, a popular technique that is often used for the analysis of a set of variables. Both PCA and 3-way PCA are aimed at summarize the information from a set of parameters in a smaller number of novel variables (also called principal components), able to express as much information as possible. But, while PCA analyzes data varying in two dimensions, 3-way PCA allows the analysis of sets of variables associated with a three-way data sets, called modes: variables, objects and conditions (for example, in case of cells photographed in different days of culture, the conditions could be the time intervals). Several models implement the 3-way PCA methodology: here the Tucker3 model is implemented.
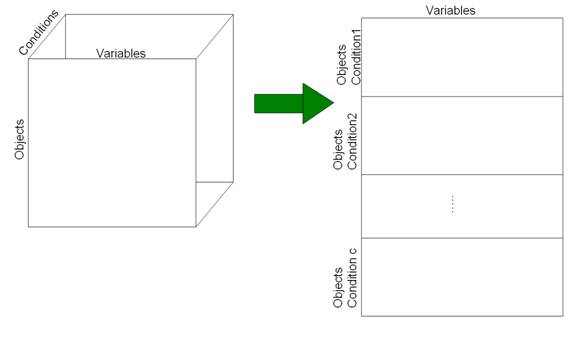
In order to perform the 3-way PCA, the data need to be organized in a matrix. This matrix is formally bi-dimensional, but contains information about all the three-modes. In fact, from an hypothetic 3D matrix, with dimension n×m×c, c matrices with dimensions n×m are extracted. Then, these matrices have to be vertically concatenated. The result is a datamatrix with structure (n×c) ×m. The figure below graphically explain the matrix organization.
User can construct this particular structure using Matlab®, and save it as a .mat file.
When user runs the plug-in, he has to select the matrix to be analyzed. After this selection, automatically an input box is displayed, where he can indicate the option to pre-process the data through a scaling (to remove standardization offsets). The number of conditions (i.e. days of cell observation) and the number of iterations also have to be indicated.
The 3-wayPCA tool delivers several plots, but the most important are three: one for objects (i.e. cells), one for variables (i.e. morphological variables extracted from cells image) and one for conditions (i.e. time intervals in which the cells are photographed). They are loading plots, so they display the parameters (variables, objects and conditions) in relation to the first two principal components, that are the most significant ones. The axes of the loading plots express these components.
Such as PCA, in order to properly interpret the 3-way PCA plots, it is essential to attribute appropriate identities to the axes. The axes interpretation is based on information obtained by prior knowledge.